I consider the original fraction: x/y.
If the numerator "x" increases by 20%, it can be interpreted in this way:
"x" represents 100% (the unit) and when increasing by 20% we have that the value of "x" becomes 120%
120% of "x" is
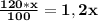
This is what we have left in the numerator.
By the same reasoning, in the denominator "y" remains:
100% - 40% = 60% of "and"
60% of "y" is...
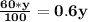
The new fraction is: 1,2x / 1,6y.
...simplifying by dividing top and bottom by 0.6,... 2x / y
To find out the percentage by which the original fraction has changed, we first find the relationship or ratio between the original fraction and the new fraction with the fraction quotient:

... that is to say that the new fraction has doubled in relation to the original.
Therefore, the percentage of variation per increase is 100%.
Pisces04