Answer:
The answer is below
Explanation:
The slope of a line (m) is given by:

Two lines are parallel if they have the same slope and perpendicular if the product of their slope is -1.
1)
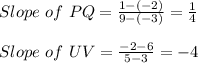
Since the product of their slope is -1, they are perpendicular
2)
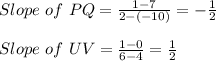
Since the slope is not the same or product of their slope is not -1, they are neither parallel or perpendicular
3)
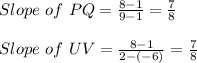
Since the slopes are the same, they are parallel
4)
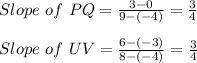
Since the slopes are the same, they are parallel
5)

Since the product of their slope is -1, they are perpendicular