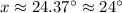Question

PLEASE OF YOU CAN SHOW THE WORK:

The accompanying diagram shows a flagpole that stands on level ground. Two cables, r and s, are attached to a pole at a point 20 feet above the ground. The combine length of the two cables is 70 feet. If cable r is attached to the ground 8 feet from the base of the pole, what is the measure of the angle, x, to the nearest degree, that cable s makes with the ground? N = 20 ft S 8 t​

Answer 1

`x\approx24^\circ`

Explanation:

We know that r and s have a combined length of 70. Therefore:

`r+s=70`

Notice that we can determine r by using the Pythagorean Theorem. In this case, r is the hypotenuse, and 20 and 8 are the legs. Therefore:

`a^2+b^2=c^2`

Substituting 20 and 8 for a and b and r for c yields:

`20^2+8^2=r^2`

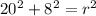
Compute:

`464=r^2`

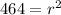
Therefore:

`r=√(464)=√(16\cdot 29)=4√(29)`

Now, we can determine s. We know that:

`s+r=70`

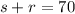
So, by substitution:

`s+4√(29)=70`

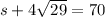
Therefore:

`s=70-4√(29)`

Now, notice that, with respect to x, 20 is the opposite side and s is the hypotenuse.

Therefore, we can use the sine ratio. The sine ratio is the ratio between a right triangles opposite side to its hypotenuse.

In this case, the opposite to x is 20, and the hypotenuse is s, or 70-4√29. Therefore:

`\displaystyle \sin(x^\circ)=(20)/(s)`

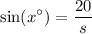
By substitution:

`\displaystyle \sin(x^\circ)=(20)/(70-4√(29))`

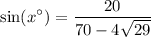
Take the inverse sine of both sides:

`\displaystyle x^\circ=\sin^(-1)\Big((20)/(70-4 √(29)) \Big)`

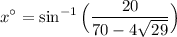
Use a calculator. Therefore:

`x\approx24.37^\circ\approx24^\circ`