Question

Find the maxima and minima of the following function:


`\displaystyle f(x) = (x^2 - x - 2)/(x^2 - 6x + 9)`

Answer 1

`\text{Minimum at }\left((7)/(5),-(9)/(16)\right)`

Explanation:

The local maximum and minimum points of a function are stationary points (turning points). Stationary points occur when the gradient of the function is zero. Differentiation is an algebraic process that finds the gradient of a curve.

To find the stationary points of a function:

• Differentiate f(x)
• Set f'(x) = 0
• Solve f'(x) = 0 to find the x-values
• Put the x-values back into the original equation to find the y-values.

`\boxed{\begin{minipage}{5.5 cm}\underline{Quotient Rule for Differentiation}\\\\If $y=(u)/(v)$ then:\\\\$\frac{\text{d}y}{\text{d}x}=\frac{v \frac{\text{d}u}{\text{d}x}-u\frac{\text{d}v}{\text{d}x}}{v^2}$\\\end{minipage}}`

`\text{Given function}: \quad \text{f}(x)=(x^2-x-2)/(x^2-6x+9)`

Differentiate the function using the Quotient Rule:

`\text{Let }u=x^2-x-2 \implies \frac{\text{d}u}{\text{d}x}=2x-1`

`\text{Let }v=x^2-6x+9 \implies \frac{\text{d}v}{\text{d}x}=2x-6`

`\begin{aligned}\implies \frac{\text{d}y}{\text{d}x} & =((x^2-6x+9)(2x-1)-(x^2-x-2)(2x-6))/((x^2-6x+9)^2)\\\\& =((2x^3-13x^2+24x-9)-(2x^3-8x^2+2x+12))/((x^2-6x+9)^2)\\\\\implies \text{f}\:'(x)& =(-5x^2+22x-21)/((x^2-6x+9)^2)\\\\\end{aligned}`

Set the differentiated function to zero and solve for x:

`\begin{aligned}\implies \text{f}\:'(x)& =0\\\\\implies (-5x^2+22x-21)/((x^2-6x+9)^2) & = 0\\\\-5x^2+22x-21 & = 0\\\\-(5x-7)(x-3) & = 0\\\\\implies 5x-7 & = 0 \implies x=(7)/(5)\\\\\implies x-3 & = 0 \implies x=3\end{aligned}`

Put the x-values back into the original equation to find the y-values:

`\implies \text{f}\left((7)/(5)\right)=(\left((7)/(5)\right)^2-\left((7)/(5)\right)-2)/(\left((7)/(5)\right)^2-6\left((7)/(5)\right)+9)=-(9)/(16)`

`\implies \text{f}(3)=(\left(3\right)^2-\left(3\right)-2)/(\left(3\right)^2-6\left(3\right)+9)=(4)/(0) \implies \text{unde}\text{fined}`

Therefore, there is a stationary point at:

`\left((7)/(5),-(9)/(16)\right)\:\text{only}`

To determine if it's a minimum or a maximum, find the second derivative of the function then input the x-value of the stationary point.

• If f''(x) > 0 then its a minimum.
• If f''(x) < 0 then its a maximum.

Differentiate f'(x) using the Quotient Rule:

Simplify f'(x) before differentiating:

`\begin{aligned}\text{f}\:'(x) & =(-5x^2+22x-21)/((x^2-6x+9)^2)\\\\& = (-(5x-7)(x-3))/(\left((x-3)^2\right)^2)\\\\& = (-(5x-7)(x-3))/((x-3)^4)\\\\& = -((5x-7))/((x-3)^3)\\\\\end{aligned}`

`\text{Let }u=-(5x-7) \implies \frac{\text{d}u}{\text{d}x}=-5`

`\text{Let }v=(x-3)^3 \implies \frac{\text{d}v}{\text{d}x}=3(x-3)^2`

`\begin{aligned}\implies \frac{\text{d}^2y}{\text{d}x^2} & =(-5(x-3)^3+3(5x-7)(x-3)^2)/((x-3)^6)\\\\& =(-5(x-3)+3(5x-7))/((x-3)^4)\\\\\implies \text{f}\:''(x)& =(10x-6)/((x-3)^4)\end{aligned}`

Therefore:

`\text{f}\:''\left((7)/(5)\right)=(625)/(512) > 0 \implies \text{minimum}`

Answer 2

To find the maxima and minima of the function, we need to calculate the derivative of the function. Note, before the denominator is a perfect square trinomial, so the function can be simplified as

`\large\displaystyle\text{$\begin{gathered}\sf \bf{\displaystyle f(x) = (x^2 - x - 2)/((x - 3)^2)} \end{gathered}$}`

So the derivative is:

`\large\displaystyle\text{$\begin{gathered}\sf \bf{\displaystyle f'(x) = ((2x - 1)(x - 3)^2 - 2(x - 3)(x^2 - x - 2))/((x - 3)^4) } \end{gathered}$}`

Simplifying the numerator, we get:

`\large\displaystyle\text{$\begin{gathered}\sf \bf{\displaystyle f'(x) = ((x - 3)(-5x + 7))/((x - 3)^4) = (-5x + 7)/((x - 3)^3) } \end{gathered}$}`

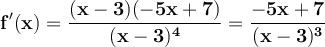
The function will have a maximum or minimum when f'(x) = 0, that is,

`\large\displaystyle\text{$\begin{gathered}\sf \bf{\displaystyle f'(x) = (-5x + 7)/((x - 3)^3) = 0 } \end{gathered}$}`

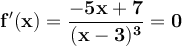
which is true if -5x + 7 = 0. Then x = 7/5.

To determine whether x = 7/5 is a maximum, we can use the second derivative test or the first derivative test. In this case, it is easier to use the first derivative test to avoid calculating the second derivative. For this, we evaluate f'(x) at a point to the left of x = 7/5 and at a point to the right of it (as long as it is not greater than 3). Since 1 is to the left of 7/5, we evaluate:

`\large\displaystyle\text{$\begin{gathered}\sf \bf{\displaystyle f(1) = (-5 + 7)/((1 - 3)^3) = (2)/(-8) < 0} \end{gathered}$}`

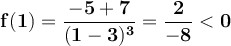
Likewise, since 2 is to the right of 7/5, then we evaluate:

`\large\displaystyle\text{$\begin{gathered}\sf \displaystyle \bf{(-10 + 7)/((2 - 3)^3) = (-3)/(-1) > 0} \end{gathered}$}`

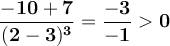
Note that to the left of 7/5 the derivative is negative (the function decreases) and to the right of 7/5 the derivative is positive (the function increases).

The value of f(x) at 7/5 is:

`\large\displaystyle\text{$\begin{gathered}\sf \bf{\displaystyle f\left(\tfrac{7}{5}\right) = \frac{\tfrac{49}{25} - \tfrac{7}{5} - 2}{\tfrac{49}{25} - 6 \cdot \tfrac{7}{5} + 9} = -(9)/(16) } \end{gathered}$}`

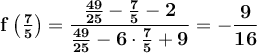
This means that
`\bf{\left( (7)/(5), -(9)/(16) \right)}` is a minimum (and the only extreme value of f(x)).

`\huge \red{\boxed{\green{\boxed{\boldsymbol{\purple{Pisces04}}}}}}`