Answer:
x=12
Explanation:
Given that there is only one expression given in each triangle, if we only use the information in a single triangle, there is no way to set up an equation that we could solve to find the expression. (For this situation, at best we could use the triangle sum theorem to say that the three angles in one triangle added to 180°, but since we don't know the other two angles, that's 3 unknowns with only 1 equation... that's not solvable)
The only way to solve this problem is to make a relationship of some sort between the two triangles.
Proving a relationship between triangles - option 1
You may have a theorem about the Third angles of two triangles... "Given two arbitrary triangles,
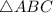 and
and
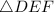 , if
, if
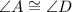 and
and
 , then
, then
 "
"
If you have this, then the third angles are congruent.
In a more general situation of a similar problem (one in which you don't know two of the angles to begin with), it might be easier to prove triangle congruence, or triangle similarity.
Other Relationships between triangles
There are two main relationships between triangles: similarity and congruence.
Most people learn about congruence first.
In the situation for this problem, the two triangles happen to be congruent (we'll prove it shortly), which implies that all corresponding angles between shapes are congruent (and all corresponding sides between shapes are congruent).
For the purpose of solving for things related to angles, proving that the two triangles are similar is enough to know that angles between triangles are congruent (sides wouldn't necessarily be equal, but would be proportional, and since we're not solving for anything related to side lengths, proving that the triangles are similar would be enough).
Proving a relationship between triangles - option 2 - congruence
Notice that the triangle on top has two angles with markings (a single mark, and a double mark), and one side with a marking (a single tick). These three pieces are in a configuration of ASA (the side is between the two angles).
Looking at the bottom triangle, it also has angles and sides with corresponding markings, and they are also in an ASA configuration.
Thus, by ASA congruence, these triangles are congruent triangles.
Knowing the triangles are congruent (even though we only used 3 parts), the rest of the corresponding parts (including the third angles) are also congruent.
Proving a relationship between triangles - option 3 - Similarity
For similarity, the process is similar to proving congruence, however the theorems we have for proving similarity are different.
SSS, SAS, or AA similarity.
Since the triangles in our problem do have two angles that are congruent, by AA similarity, the triangles are "similar".
Knowing the triangles are similar (even though we only used 2 parts), the last set of corresponding angles are also congruent.
Building our equation
Since the third angle of each triangle is congruent, by definition of congruent angles, the measures of each of those two angles are equal, and so we can build an equation knowing that the two expressions are equal to each other:
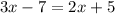
Solving for x
From there, we need some algebraic properties equality to solve for x.
Subtract 2x from both sides...

add 7 to both sides...
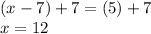
Extension
Knowing the value for x, we could solve for the measure of the angles, if that had been requested. Simply substitute 12 back into the expressions for the angle measure (the results should be the same for both angles, since they were congruent angles)


So, if we had been asked, the measure of the angle is 29°