Answer:
c.)

Explanation:
The given expression is written in the form
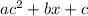 . To factor, find two numbers whose sum is b and whose product is c:
. To factor, find two numbers whose sum is b and whose product is c:
_×_=-18
_+_=7
Use -2 and 7:
-2×9=-18
-2+9=7
Substitute the two numbers for b:
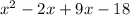
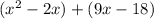
Factor out common terms. The common term in the first parentheses is x and the common term in the second is 9:
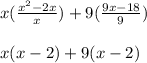
Cancel out one of the parentheses since they have the same terms and plug the factored numbers in:
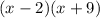
:Done
Check Your Work:
To see if the given factored form is true, simplify it using FOIL:
First, Outside, Inside, Last
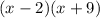
Multiply the first terms:
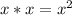
Multiply the terms on the outside:
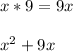
Multiply the inside terms:
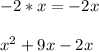
Multiply the last terms:

Combine like terms:
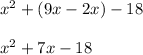
Therefore, the factored form is true.