To find the maxima and minima of the function, we need to calculate the derivative of the function. Note, before the denominator is a perfect square trinomial, so the function can be simplified as
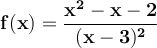
So the derivative is:
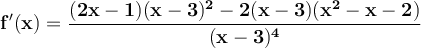
Simplifying the numerator, we get:
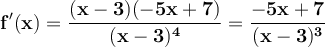
The function will have a maximum or minimum when f'(x) = 0, that is,
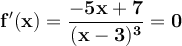
which is true if -5x + 7 = 0. Then x = 7/5.
To determine whether x = 7/5 is a maximum, we can use the second derivative test or the first derivative test. In this case, it is easier to use the first derivative test to avoid calculating the second derivative. For this, we evaluate f'(x) at a point to the left of x = 7/5 and at a point to the right of it (as long as it is not greater than 3). Since 1 is to the left of 7/5, we evaluate:
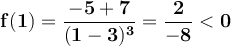
Likewise, since 2 is to the right of 7/5, then we evaluate:
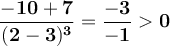
Note that to the left of 7/5 the derivative is negative (the function decreases) and to the right of 7/5 the derivative is positive (the function increases).
The value of f(x) at 7/5 is:
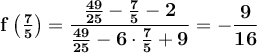
This means that
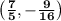 is a minimum (and the only extreme value of f(x)).
is a minimum (and the only extreme value of f(x)).
