Question

A triangle is inscribed in a rectangle if each vertex of the triangle lies on a side of or at a vertex of the rectangle. This diagram shows shaded triangle ACE inscribed in rectangle ABDE. Find the number of square units in the area of shaded triangle ACE, if the area of the rectangle is 13.5 square units

Answer 1

ITS MATH OLYMPIAD 2020 DEC 14

Step-by-step explanation:

HI

Answer 2

The area of the shaded triangle ACE inscribed in rectangle ABDE is 6.75 square units. This is calculated by recognizing that the area of a triangle inscribed in a rectangle is half the area of the rectangle, and applying this relationship to the given area of the rectangle (13.5 square units).

Step-by-step explanation:

When a triangle is inscribed in a rectangle in such a way that one side of the triangle coincides with a side of the rectangle, the triangle's area is equal to half the area of the rectangle.

The formula for the area of a triangle is
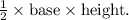`\( (1)/(2) * \text{base} * \text{height} \).` In this case, triangle ACE shares a base with the rectangle ABDE.

Given that the area of the rectangle ABDE is 13.5 square units, the formula for the area of triangle ACE is:

`\[ \text{Area of triangle ACE} = (1)/(2) * \text{base} * \text{height} \]`

Since triangle ACE and the rectangle share a common base (side AC of the rectangle), the base of triangle ACE is the same as the base of the rectangle, and the height of triangle ACE is equal to the remaining side of the rectangle (side AE). Therefore, the area of triangle ACE is given by:

`\[ \text{Area of triangle ACE} = (1)/(2) * \text{base} * \text{height} = (1)/(2) * AC * AE \]`

To calculate the numerical value, it is crucial to have specific measurements for AC and AE. Without those values, we can express the area in terms of the given area of the rectangle:

`\[ \text{Area of triangle ACE} = (1)/(2) * \text{Area of rectangle ABDE} = (1)/(2) * 13.5 = 6.75 \]`

Therefore, the detailed calculation involves recognizing the relationship between the area of a triangle inscribed in a rectangle and the rectangle's area, which is
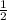`\( (1)/(2) \)` of the rectangle's area when they share a common base. In this scenario, the area of the shaded triangle ACE is 6.75 square units.