Answer:
The rule of dilation is
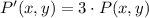 .
.
The vertices of the dilated triangle are
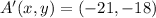 ,
,
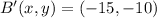 and
and
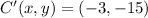 , respectively.
, respectively.
Explanation:
From Linear Algebra, we define the dilation by the following definition:
![P'(x,y) = O(x,y) + k\cdot[P(x,y)-O(x,y)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/u2i0kxamv233cf3vl32ee3m7xvasp6gj1d.png) (1)
(1)
Where:
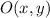 - Center of dilation, dimensionless.
- Center of dilation, dimensionless.
 - Scale factor, dimensionless.
- Scale factor, dimensionless.
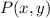 - Original point, dimensionless.
- Original point, dimensionless.
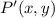 - Dilated point, dimensionless.
- Dilated point, dimensionless.
If we know that
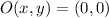 ,
,
 ,
,
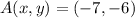 ,
,
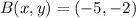 and
and
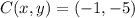 , then dilated points of triangle ABC are, respectively:
, then dilated points of triangle ABC are, respectively:
![A'(x,y) = O(x,y) + k\cdot [A(x,y)-O(x,y)]](https://img.qammunity.org/2021/formulas/mathematics/college/58b91kawxm2zyrilhgaes3594f1ghis3vz.png) (2)
(2)
![A'(x,y) = (0,0) + 3\cdot [(-7,-6)-(0,0)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/kmf0y34hfddalt70at4ed6zmax5wi820lk.png)
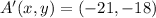
![B'(x,y) = O(x,y) + k\cdot [B(x,y)-O(x,y)]](https://img.qammunity.org/2021/formulas/mathematics/college/sjlbn74gdkj7avbshw7dznl3dxevssbqzp.png) (3)
(3)
![B'(x,y) = (0,0) + 3\cdot [(-5,-2)-(0,0)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/z4tb3e1wx153jed4bpgm0jc5u9b4krvh2j.png)
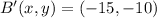
![C'(x,y) = O(x,y) + k\cdot [C(x,y)-O(x,y)]](https://img.qammunity.org/2021/formulas/mathematics/college/xg453j8s2ndbaiyw2hla34tst5dz0se83h.png) (4)
(4)
![C'(x,y) = (0,0) +3\cdot [(-1,-5)-(0,0)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/tcichxlgvijnc68obdgt05nxa2fmetn54r.png)
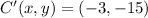
The rule of dilation is:
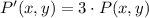 (5)
(5)
The vertices of the dilated triangle are
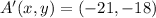 ,
,
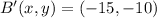 and
and
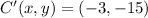 , respectively.
, respectively.