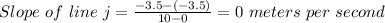Question

An oil-well contractor drills a shaft 7 meters deeper into the ground every 2 hours. Which graph has a slope that best represents this rate?

Answer 1

Answer:The answer is H , It is the graph where -10 is right below the 0 on the y.

Answer 2

Graph G

Explanation:

The graphs are attached

Given that the oil-well contractor drills a shaft 7 meters deeper into the ground every 2 hours, hence the rate at which the shaft drills = 7 meter / 2 hours = 3.5 meters per hour

Since the drill goes into the ground, hence the rate is negative that is -3.5 meters per secong

The slope (rate of change) of a line (m) is given by:

`m=(y_2-y_1)/(x_2-x_1)`

a) For graph F, the line passes through the point (0,0) and (10, -20). Hence:

`Slope\ of\ line\ F=(-20-0)/(10-0) =-2\ meters\ per\ second`

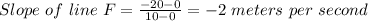
b) For graph G, the line passes through the point (0,0) and (10, -70). Hence:

`Slope\ of\ line\ G=(-70-0)/(10-0) =-7\ meters\ per\ second`

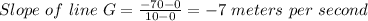
c) For graph H, the line passes through the point (0,0) and (10, -35). Hence:

`Slope\ of\ line\ H=(-35-0)/(10-0) =-3.5\ meters\ per\ second`

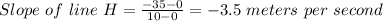
d) For graph J, the line passes through the point (0,-3.5) and (10, -3.5). Hence:

`Slope\ of\ line\ j=(-3.5-(-3.5))/(10-0) =0\ meters\ per\ second`