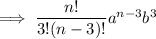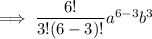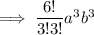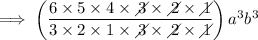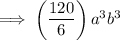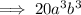Question

What is the fourth term in the binomial expansion (a+b)^6)

Answer 1

`20a^3b^3`

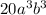
Explanation:

Binomial Series

`(a+b)^n=a^n+(n!)/(1!(n-1)!)a^(n-1)b+(n!)/(2!(n-2)!)a^(n-2)b^2+...+(n!)/(r!(n-r)!)a^(n-r)b^r+...+b^n`

Factorial is denoted by an exclamation mark "!" placed after the number. It means to multiply all whole numbers from the given number down to 1.

Example: 4! = 4 × 3 × 2 × 1

Therefore, the fourth term in the binomial expansion (a + b)⁶ is:

`\implies (n!)/(3!(n-3)!)a^(n-3)b^3`

`\implies (6!)/(3!(6-3)!)a^(6-3)b^3`

`\implies (6!)/(3!3!)a^(3)b^3`

`\implies \left((6 * 5 * 4 * \diagup\!\!\!\!3 * \diagup\!\!\!\!2 * \diagup\!\!\!\!1)/(3 * 2 * 1 * \diagup\!\!\!\!3 * \diagup\!\!\!\!2 * \diagup\!\!\!\!1)\right)a^(3)b^3`

`\implies \left((120)/(6)\right)a^(3)b^3`

`\implies 20a^3b^3`