Answer: The answer is x < 5/2 and x > -5.
Explanation:
First you need to separate the inequality and keep x on one side to maintain consistency. For instance the problem-
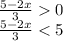
Now solve as normal.
*Note: When dividing a side or multiplying a side by a negative number, the sign of the inequality switches (this will be shown when I do the equation if it doesn't make since how I word it).
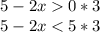
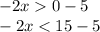
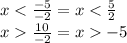
So, x < 5/2 and x > -5.
If anything is confusing about the procedure just leave a comment, and I'll try to explain further.