Question

Can a regular polygon have an interior angle of 132 degrees?

Answer 1

Given:

The interior angle of a regular polygon is 132 degrees.

To find:

The given statement is possible or not.

Solution:

Let as assume the interior angle of a regular polygon with n vertices is 132 degrees.

Then, the exterior angles are

`180^\circ-132^\circ=48^\circ`

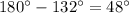
We have, n vertices. So, the number of exterior angles is n.

Sum of all exterior angles = 48n degrees

We know that, sum of all exterior angles of a regular polygon is always 360 degrees.

`48n=360`

`n=(360)/(48)`

`n=7.5`

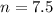
Number of vertices is always a whole number. So, it cannot be a fraction value.

So, our assumption is wrong.

Therefore, a regular polygon cannot have an interior angle of 132 degrees.