Answer:
Short leg: 9 in
Long leg: 40 in
Hypotenuse: 41 in
Explanation:
This problem involves the Pythagorean Theorem, solving a system of equations, and solving a quadratic equation.
The Pythagorean Theorem applies because the question states this is a right triangle. That is one equation.
Two more equations come from descriptive relationships between various sides of the triangle.
Solving the system is done here with the Substitution Method, and solving the quadratic equation is done with factoring and the zero product property. Other methods could be used, but there is a character limit, so we can't dive into every way to solve this.
The Pythagorean Theorem
Pythagorean Theorem:
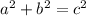 where "c" is the hypotenuse of the right triangle.
where "c" is the hypotenuse of the right triangle.
"c" must be hypotenuse.
It doesn't matter which of the two legs' lengths is used for "a" & "b". However, because of other parts of the question, we'll need to know which one is which.
The question refers back multiple times to one specific leg (the short one). So, when we refer back to that leg in our equations, we need to make sure we're using the same leg each time.
Keeping track of which leg is which
Let's use "a" for the smaller leg, and "b" for the longer leg.
"c", as always, is the hypotenuse.
Setting up the relationships between the sides
Next, the question gives two statements relating the side lengths of the triangle to each other.
For the first statement, "the length of the longer leg of a right triangle" (that's "b") "...is 13 inches more than three times the length of the shorter leg ("a").
Translating the first sentence into math:
- "the length of the longer leg of a right triangle" means "b"
- "...is..." means "="
- "...13 inches more than..." means " +13 " (start with what's coming next, and then do the adding)
- "...three times..." means " 3* "
- "... the length of the shorter leg." means "a".
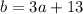
Similarly from the second statement, we get:
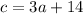
Combining this with the Pythagorean Theorem, we have a system of 3 equations, and 3 unknowns.
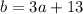
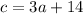
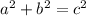
Solving a system of equations
To solve a system of equations, there are two main methods:
- The substitution method
- The elimination method
Either method can be used, but the substitution method is the most intuitive.
Substitution method
To solve a system with the substitution method, isolate variable in an equation, written in terms of the other variables, and substitute them in to try to get a single equation with a single unknown.
Looking at our system, the first two equations already have "b" and "c" isolated in terms of "a". If we substitute both of these into the third equation, we'll have a single equation in terms of a, and can attempt to solve it.
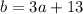
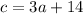
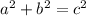
Substituting...
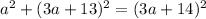
Rewrite the square binomials as a product...
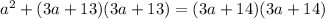
Apply FOIL (a combination of the distributive property, the commutative properties of multiplication, and combining like terms)...
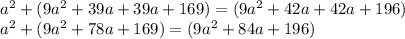
Observe that the equation is a degree-2 polynomial (polynomial with highest power of 2; aka quadratic). Move all terms to one side to get the equation equal to zero in preparation for solving:
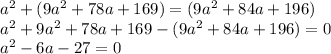
There are a few ways to solve this, including the quadratic formula. However, factoring the polynomial and using the zero product property is quite efficient here:
Factoring to solve a Quadratic
Since the leading coefficient is 1, we can use the shortcut and find factors of -27 that add to make -6.
-27 has factor pairs of:
- 1 and -27
- 3 and -9
- 9 and -3
- 27 and -1
3 and -9 add to make -6, so factoring the polynomial is
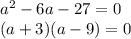
Applying the zero product property...
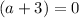 or
or
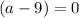
So a=-3 or a=9. Given that this represents a length in a triangle, we discard the negative solution. So a=9.
Finding the other two unknowns
To finish up, substitute the "a" back into the two equations for "b" and "c".
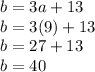
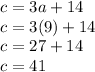
The original problem set up our measurements in inches, so all three values are measured in inches.
Remember which length was which
"a": short leg
"b": longer leg
"c": hypotenuse
Short leg: 9 in
Long leg: 40 in
Hypotenuse: 41 in.