Answer:
a) positive real zeros: 2 or 0; negative real zeros: 2 or 0; complex zeros: 0, 2, or 4. (rule of signs)
b) ∪-shaped, as for an even-degree polynomial with positive leading coefficient. See attached.
c, d) See attached
Explanation:
Descarte's rule of signs gives bounds on the number of positive and negative real roots. The numbers it gives may be reduced by multiples of 2, as complex roots will come in conjugate pairs. The total number of roots of all kinds will match the degree of the polynomial.
Synthetic division is essentially polynomial long division with some modifications:
- the variables are omitted ("place value" is used instead)
- the constant in the divisor is negated so its product with the partial quotient can be added to obtain the new dividend
- the divisor binomial is assumed to have a leading coefficient of 1.
__
a)
The signs of the terms of the given polynomial are + - - - +. There are two sign changes, so 2 possible positive real roots.
When the signs of the odd-degree terms are changed, the signs become + + - + +. There are still two sign changes, so 2 possible negative real roots.
Either or both of these numbers can be reduced by 2 if the roots include a conjugate pair. That is, there may also be 0 possible positive real roots, and 0 possible negative real roots.
The number of non-real (complex) zeros may be any multiple of 2 up to the degree of the polynomial. The may be 0, 2, or 4 possible non-real zeros.
__
b)
The graph is the first attachment. It shows 4 real zeros: x = -4, -2, 1, 6.
Since the polynomial is of even degree (4) and has a positive leading coefficient (+1), we expect the general shape to be ∪-shaped. It is.
__
c)
The second attachment shows synthetic division using x = -4. (The binomial divisor is (x+4).) The remainder (lower right value in the tableau) is the value of y when x=-4. The third attachment shows synthetic division using the value x=3. (y is -210 when x=3.)
Maybe this is the table you want:
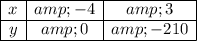
__
d)
The second attachment shows synthetic division by the factor (x+4).
_____
Additional comment
The synthetic division attachments show instructions for carrying out the synthetic division and interpreting the results. As we said above, "the entry on the left" is the opposite of the constant in the binomial divisor. It is the actual value of x you want to use to evaluate the function.
The equations shown are merely for the purpose of indicating the operations that are used. An actual synthetic division tableau is simply a 3-row table of numbers, with the bottom row being the quotient coefficients and remainder.