Answer:
Given the equation
P is the amount of profit made. So willing to find how much x you can charge to make at least 125, you have to equate P with 125 because they are both profits
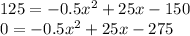
Now we are going to introduce Quadratic Formula to find the amount of x
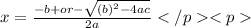

X = 16.33974596
Therefore 16.34 Dollars is the smallest amount you can charge to make the profit of 125 Dollars