Question

I want to verify my work answer for the below SSAT question.

Thank you

Cindy throws a rock in the air. The rock's height, y, in feet, with respect to time, x, in seconds can be modeled by the function y=-2x^2+10x+28. When does the rock hit the ground in seconds

My work:
y=-2x^2+10x+28
0= -2(x^2-5x-14) (While knowing that the zero is supposed to be there, I don't understand why 0= -2(x^2-5x-14) )
(x-7)(x+2)
(-7,+2)
I put 2 as the answer, but when checking it was 7?

What part did I do wrong?

Answer 1

7

Explanation:

You were correct in setting the equation equal to 0 because the problem is asking for when the rock hits the ground and in this problem, you may assume that the ground is y=0, unless the problem says otherwise.

Ok so where you went wrong is that when you factored out and got

(x-7)(x+2), which is correct, you forgot to set these equal to zero (because your actual equation is set to zero). So you should have

x-7 = 0

and

x+2 = 0

and this gives the actual answers +7 and -2. And since time cant be negative its 7 seconds.

This was a silly mistake and happens a lot more often than you think, so I wouldn't worry too much but make sure you practice more, better to lose points on harder questions than easy ones.

Good luck with your exam !

Answer 2

7 seconds

Explanation:

Given function:

`y=-2x^2+10x+28`

where:

• y = height above the ground (in feet)
• x = time (in seconds)

To find the time when the rock hits the ground, set the equation to zero and solve for x.

First, simplify by factoring out the common term -2:

`\implies -2(x^2-5x-14)=0`

Divide both sides by -2:

`\implies x^2-5x-14=0`

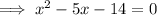
To factor a quadratic in the form
`ax^2+bx+c`, find two numbers that multiply to ac and sum to b.

`\implies ac=1 \cdot -14=-14`

`\implies b=-5`

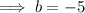
Therefore, the two numbers that multiply to -14 and sum to -5 are: -7 and 2

Rewrite b as the sum of these two numbers:

`\implies x^2-7x+2x-14=0`

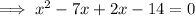
Factorize the first two terms and the last two terms separately:

`\implies x(x-7)+2(x-7)=0`

Factor out the common term (x - 7):

`\implies (x+2)(x-7)=0`

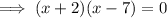
Therefore:

`\implies x+2=0 \implies x=-2`

`\implies x-7=0 \implies x=7`

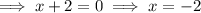
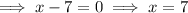
As time cannot be negative, the rock hits the ground in 7 seconds.