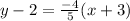Answer:
slope-intercept:
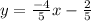
point-slope:
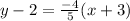
Explanation:
The slope-intercept form of a line is written as y = mx + b, where m is the slope and b is the y-intercept.
The point-slope form of a line is written as y - y1 = m(x - x1), where (x1, y1) is a given point and m is the slope.
Here, we see that the slope is -4/5, which means that m = -4/5. Since we're given a point (-3, 2), let's go ahead and just write the point-slope form already. (x1, y1) = (-3, 2) so x1 = -3 and y1 = 2. Then:
y - y1 = m(x - x1)
y - 2 = (-4/5) * (x + 3)
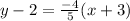
Now, we want to find the slope-intercept form, so we need to figure out the y-intercept. Well, first, let's plug in what we know:
y = mx + b
y = (-4/5)x + b
Any point on this line will satisfy the above equation. Since (-3, 2) is on this line, if we plug -3 in for x and 2 in for y, the equation should hold true, so we can solve for b:
y = (-4/5)x + b
2 = (-4/5) * (-3) + b
2 = 12/5 + b
b = -2/5
So, the y-intercept is -2/5. Then the slope-intercept form is:
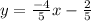
Thus, our two equations are:
slope-intercept:
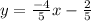
point-slope: