(a) If
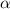 and
and
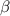 are roots of
are roots of
 , then we can factorize
, then we can factorize
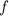 as
as
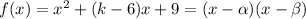
Expand the right side and match up coefficients:
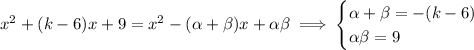
Now, recall that
 . It follows that
. It follows that
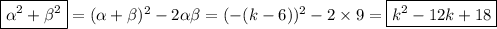
and

(b) If
 , then
, then
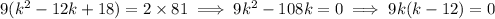
Since
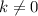 , it follows that
, it follows that
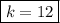 .
.
(c) The simplest quadratic expression with roots
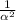 and
and
 is
is
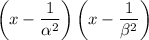
which expands to
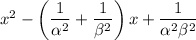
Reusing the identity from (a-i) and the result from part (b), we have
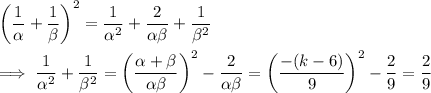
We also know from part (a-ii) that
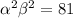 .
.
So, the simplest quadratic that fits the description is
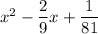
To get one with integer coefficients, we multiply the whole expression by 81 to get
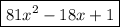 .
.