Question

Obtain derivatives of x/sinx​

Answer 1

`\displaystyle (x)/(\sin x) = \sum^(\infty)_(n = 0) ((2n + 1)!)/((-1)^nx^(2n))`

General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Sequences

Series

Taylor Polynomials

• MacLaurin Polynomial:
  `\displaystyle P_n(x) = (f(0))/(0!) + (f'(0))/(1!)x + (f''(0))/(2!)x^2 + (f'''(0))/(3!)x^3 + \cdots + (f^n(0))/(n!)x^n + \cdots`

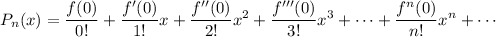
Power Series

• Power Series of Elementary Functions
• MacLaurin Series
• Taylor Series

Step-by-step explanation:

*Note:

You could derive the Taylor Series for sin(x) using Taylor polynomials by differentiation by usually you have it memorized.

We want to obtain an infinite amount of derivatives of the given:

`\displaystyle (x)/(\sin x)`

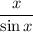
We know that a power series is defined as an infinite derivatives of a function. We know that the power series for sin(x) is:

`\displaystyle \sin x = \sum^(\infty)_(n = 0) ((-1)^nx^(2n + 1))/((2n + 1)!)`

Divide x by the power series to obtain our derivatives:

`\displaystyle (x)/(\sin x) = \sum^(\infty)_(n = 0) (x)/(((-1)^nx^(2n + 1))/((2n + 1)!))`

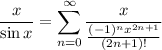
Simplify this down:

`\displaystyle (x)/(\sin x) = \sum^(\infty)_(n = 0) ((2n + 1)!)/((-1)^nx^(2n))`

And we have our final answer.

Topic: AP Calculus BC (Calculus I + II)

Unit: Power Series