Question

A piece of charcoal used for cooking is found at the remains of an ancient campsite. A 0.8 kg sample of carbon from the wood has an activity of 1770 decays per minute. Find the age of the charcoal. Living material has an activity of 15 decays/minute per gram of carbon present and the half-life of 14C is 5730 y. Answer in units of y

Answer 1

t = 15825.11 years

Explanation:

From the given information:

We can make use of the activity of the sample present after time "t" to determine the age of the sample.

This can be expressed by the formula:

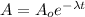`A = A_o e^(-\lambda t)` --- (1)

where;

`A_o`= activity of the sample at time t = 0

`\lambda` = disintegration constant

`\lambda = (0.693)/(T_(1/2))`

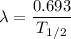
If we replace the value of
`\lambda` into equation (1), we have:

`A = A_o e^{ \Bigg [ -{ (0.693)/(T_(1/2)) \Bigg ] } t}`

`(A)/(A_o) = e^{ \Bigg [ -{ (0.693)/(T_(1/2)) \Bigg ] } t}`

By rearrangement:

`t = (-T_(1/2) In ((A)/(A_o)))/(0.693)`

`t = - (\left(5730\ \cdot\ \ln\left((\left(1770\right))/(0.8\cdot10^(3)\cdot15)\right)\right))/(0.693)`

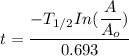
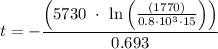
t = 15825.11 years