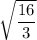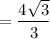Answer:
This is a sphere with a center
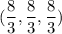 and radius
and radius
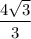
Explanation:
Given that: (x,y,z)
where;
d₁ is the distance from the origin =

d₂ is the distance from (2,2,2) =
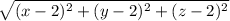
Also;
d₁ = 2d₂

By squaring both sides;
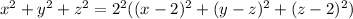
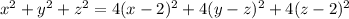
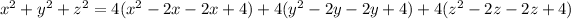
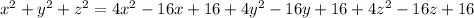
Collect the like terms:
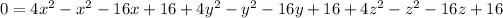
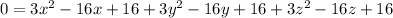
Divide both sides by 3


Using the completing the square method;
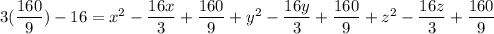
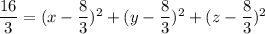
∴
This is a sphere with a center
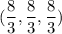 and ;
and ;
radius;