Question

A 5.50-kg object is hung from the bottom end of a vertical spring fastened to an overhead beam. The object is set into vertical oscillations having a period of 3.50 s. Find the force constant of the spring.

Answer 1

17.71N/m

Step-by-step explanation:

The period of the spring is expressed according to the expression;

`T = 2 \pi \sqrt{(m)/(k) } \\`

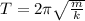
m is the mass of the object

k is the force constant

Given

m = 5.50kg

T = 3.50s

Substitute into the formula;

`T = 2 \pi \sqrt{(m)/(k) } \\3.5 = 2 (3.14) \sqrt{(5.5)/(k) } \\3.5 = 6.28 \sqrt{(5.5)/(k) } \\(3.5)/(6.28) = \sqrt{(5.5)/(k) } \\0.557 = \sqrt{(5.5)/(k) } \\square \ both \ sides\\0.557^2 = (\sqrt{(5.5)/(k) })^2 \\0.3106 = (5,5)/(k)\\k = (5.5)/(0.3106)\\k = 17.71N/m`

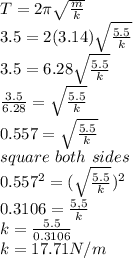
Hence the force constant of the spring is 17.71N/m