Answer:
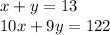
Jose worked on washing cars for 5 hours and on walking dogs for 8 hours.
Explanation:
Given that:
Jose works for two summer jobs.
Earnings per hour by the first job i.e. by washing cars = $10
Earnings per hour by the second job i.e. by walking dogs = $9
Total number of hours worked = 13 hours (30 hours does not give us proper answer, it must be 13)
Total money earned = $122
To find:
System of equations to find the number of hours that Jose worked on each job?
Solution:
Let number of hours worked on washing cars =
 hours
hours
Let number of hours worked on walking dogs =
 hours
hours
As per the question statement, we can write the following system of equations:
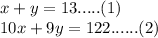
Let us use the Elimination method to find the values of
 and
and
 .
.
Multiplying the equation (1) by 10 and then subtracting the equation (2) from it:
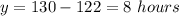
Using the equation (1):
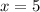 hours
hours
Therefore, Jose worked on washing cars for 8 hours and on walking dogs for 5 hours.