Answer:

Number of 2-point shots taken = 12
Number of 3-point shots taken = 6
Explanation:
Total number of points scored by Gladys = 42
Only 2-point and 3-point shots are taken by Gladys.
Let number of 2-point shots taken =

Let number of 3-point shots taken =

Total number of shots taken = 18
Therefore, first equation can be written as:
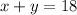
Total points scored = 42
Therefore, second equation can be written as:
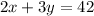
System of equations is:
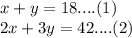
Using elimination method to solve the system of equations.
Multiplying equation by 2 then subtracting it from equation (2):
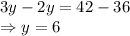
By equation (1):

Therefore, Number of 2-point shots taken = 12
Number of 3-point shots taken = 6