Question

Using the rule-of-1 approach, what is the proportional change in centripetal acceleration, ac, for an object in a circular path when the tangential velocity is doubled? 2ac (doubles) 2 A sub c, (doubles) ac2 (halves) the fraction with numerator A sub c and denominator 2, (halves) ac4 (quarters) the fraction with numerator A sub c and denominator 4, (quarters) 4ac (quadruples)

Answer 1

4ac (quadruples)

Step-by-step explanation:

The general formula for centripetal acceleration is given as follows:

`a_(c) = (v^2)/(r)\\\\` -------------- equation (1)

where,

ac = centripetal acceleration

v = tangential speed

r = radius of circular path

Now, if we double tangential speed, v' = 2v, then the acceleration will become:

`a_(c)' = ((2v)^2)/(r)\\\\a_(c)' = (4v^2)/(r)`

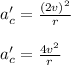
using equation (1):

`a_(c)' = 4a_(c)`

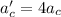
therefore, the correct answer is:

4ac (quadruples)