Answer:
5 hours
Explanation:
Given
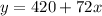 --- Revenue
--- Revenue
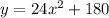 --- Overhead cost
--- Overhead cost
Required
Determine the hours for break even
To do this, we simply equate both expressions as follows:
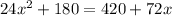
Collect Like Terms
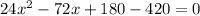
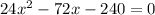
Divide through 24
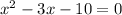
Expand:
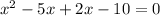
Factorize:
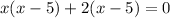
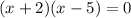
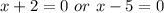
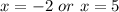
But x can't be negative because it represents time.
So, x = 5 hours