Answer:
B: 30°, 78°, 72
Explanation:
Given a
 .
.
Let
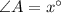
As per question statement,
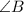 is 18° more than twice of
is 18° more than twice of
 .
.
i.e
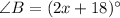
 is 42° more than that of
is 42° more than that of

To find:
The angle measures of the triangle = ?
Solution:
We can use the angle sum property of a triangle here to find the three angles of the triangle.
As per angle sum property, the sum of all the three internal angles is equal to
 .
.
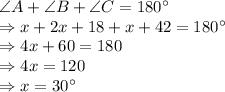
i.e.
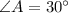
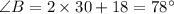

Therefore, the correct answer is:
B: 30°, 78°, 72