Question

Find the distance between the pair of points (7,6) and (4,10)​

Answer 1

5 units

Explanation:

to find out the answer for this you must first find the distance between 7 and 4 and then 6 and 10

then you would square them and then add them

lastly you would take the square root of that and youd have your answer

so

7 - 4 = 3

6 - 10 = -4 (just use 4)

3^2 + 4^2 = 9 + 16 = 25

then you take the square root of this

sqrt(25) = 5

that is your answer

Answer 2

To solve this problem, you will use the Distance Formula to find the distance between two coordinate points.

Set Up the Distance Formula

The Distance Formula is defined as follows:

`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

We must title our points by the standard coordinate naming system:

`(x_1, y_1) \ \text{and} \ (x_2, y_2)`

Therefore, our points can be labeled:

• 
  `x_1 = 7`
• 
  `y_1 = 6`
• 
  `x_2 = 4`
• 
  `y_2 = 10`

Substitute Known Values for Variables

Now, substitute the known values as the variables in the Distance Formula:

`d=√((4 - 7)^2 + (10 - 6)^2)`

You must know the BPEMDAS acronym, which stands for:

Brackets

Parentheses

Exponents

Multiplication

Division

Addition

Subtraction

Simplify the expression using BPEMDAS:

`d=√((-3)^2 + (4)^2)`

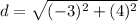
Remember that when a number is raised to the 2nd power, it is the same thing as multiplying the number by itself:

`-3*-3 = 9`

`4*4=16`

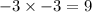
Simplify further by removing the parentheses:

`d=√(9+16)`

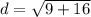
Compute the additive operation:

`d=√(25)`

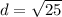
Simplify the Radicand

The number that is placed inside of a square root symbol (or a radical symbol) is referred to as the radicand.

In this situation, the radicand is 25.

To simplify the radicand, you may either use a calculator to compute the result, or you can determine which number raised to the 2nd power will result in a final answer of 25.

In this case, we can determine that 5² will result in a final answer of 25.

`5^(2) = 25`

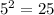
The final answer is 5 units.