Answer:
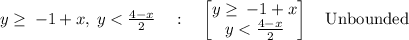
The graph is attached below.
Explanation:
Given the system of inequalities.
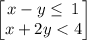
Isolate y for
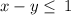
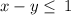
subtract x from both sides
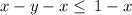
simplify
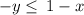
Multiply both sides by -1 (reverse the inequality)
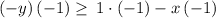
simplify
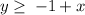
now solving
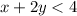
isolate y for
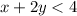
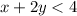
subtract x from both sides

simplify
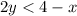
Divide both sides by 2
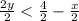
Simplify

Graphing Method:
1. Graph each inequality separately
2. Choose a test point to determine which side of the line needs to be shaded
3. The solution to the system will be the area where the shadings from each inequality overlap one another.
Thus,
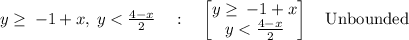
The graph is attached below.