Question

Use quadratic regression to find the

equation for the parabola going
through these 3 points.
(-7, 134) (-3, 10) (5, 50)

Answer 1

Given:

The three points are (-7,134), (-3,10) and (5,50).

To find:

The equation of parabola using quadratic regression.

Solution:

The general equation of quadratic regression is

`y=ax^2+bx+c` ...(i)

The three points are (-7,134), (-3,10) and (5,50).

Using the graphing calculator, we get a=3, b=-1 and c=-20. Putting these values in (i), we get

`y=3x^2+(-1)x+(-2)`

`y=3x^2-x-2`

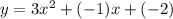
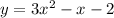
Therefore, the equation of parabola is
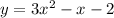`y=3x^2-x-2` and the missing values in the given equation are 3, -1 and -20.