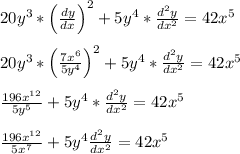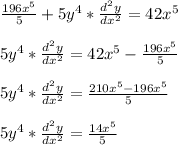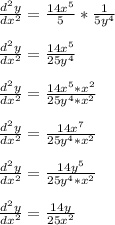Question

Find d²y/dx² in terms of x and y.
y^5 = x^7
d²y/dx² =????​

Answer 1

Answer:
`(14y)/(25x^2)`

====================================================

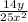
Work Shown:

First calculate
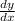`(dy)/(dx)` through the use of implicit differentiation.

Don't forget about the chain rule.

`y^5 = x^7\\\\(d)/(dx)\left[y^5\right] = (d)/(dx)\left[x^7\right]\\\\5y^4(dy)/(dx) = 7x^6\\\\(dy)/(dx) = (7x^6)/(5y^4)\\\\`

Go back to line 3, shown above, and apply the derivative to both sides.

You'll be using the product rule.

`5y^4(dy)/(dx) = 7x^6\\\\(d)/(dx)\left[5y^4(dy)/(dx)\right] = (d)/(dx)\left[7x^6\right]\\\\(d)/(dx)\left[5y^4\right]*(dy)/(dx)+5y^4*(d)/(dx)\left[(dy)/(dx)\right] = 42x^5\\\\20y^3*(dy)/(dx)*(dy)/(dx)+5y^4*(d^2y)/(dx^2)=42x^5\\\\20y^3*\left((dy)/(dx)\right)^2+5y^4*(d^2y)/(dx^2) = 42x^5\\\\`

Use substitution and isolate
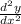`(d^2y)/(dx^2)` to get the following:

`20y^3*\left((dy)/(dx)\right)^2+5y^4*(d^2y)/(dx^2) = 42x^5\\\\20y^3*\left((7x^6)/(5y^4)\right)^2+5y^4*(d^2y)/(dx^2) = 42x^5\\\\(196x^(12))/(5y^5)+5y^4*(d^2y)/(dx^2) = 42x^5\\\\(196x^(12))/(5x^7)+5y^4(d^2y)/(dx^2) = 42x^5\\\\`

`(196x^5)/(5)+5y^4*(d^2y)/(dx^2)=42x^5\\\\5y^4*(d^2y)/(dx^2)=42x^5-(196x^5)/(5)\\\\5y^4*(d^2y)/(dx^2)=(210x^5-196x^5)/(5)\\\\5y^4*(d^2y)/(dx^2)=(14x^5)/(5)\\\\`

`(d^2y)/(dx^2)=(14x^5)/(5)*(1)/(5y^4)\\\\(d^2y)/(dx^2)=(14x^5)/(25y^4)\\\\(d^2y)/(dx^2)=(14x^5*x^2)/(25y^4*x^2)\\\\(d^2y)/(dx^2)=(14x^7)/(25y^4*x^2)\\\\(d^2y)/(dx^2)=(14y^5)/(25y^4*x^2)\\\\(d^2y)/(dx^2)=(14y)/(25x^2)\\\\`