Answer:
The solution of this system of linear equations is
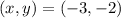 .
.
Explanation:
Let be the following system of linear equations:
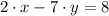 (1)
(1)
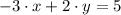 (2)
(2)
From (1) we clear
 :
:
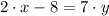
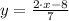
And we apply this variable in (2):
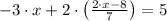
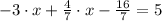
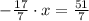
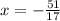

And the value of
 is:
is:
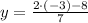
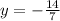
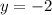
The solution of this system of linear equations is
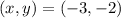 .
.