Answer:
93
Explanation:
Let the digit in tens place be 'x' & digit in ones place be 'y'.
So , the original number =
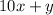
According to the question ,
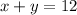 ......... .eqn(1)
......... .eqn(1)
When digits are interchanged ,
The new number formed =
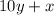
According to the question ,
 ............ eqn(2)
............ eqn(2)
Solving eqn(2) further ,
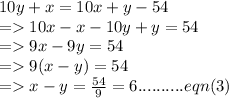
Adding eqn(1) and eqn(3) ,

Putting the value of x in eqn(1),

∴ Original number = 93