Question

Find the range of the following piecewise function.

[0,11)
(-4,6]
(0,11]
[-4,6)

Answer 1

Given:

The piecewise function is

`f(x)=\begin{cases}x+4 & \text{ if } -4\leq x<3 \\ 2x-1 & \text{ if } 3\leq x<6 \end{cases}`

To find:

The range of given piecewise function.

Solution:

Range is the set of output values.

Both functions
`f(x)=x+4` and
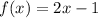`f(x)=2x-1` as linear functions.

Starting value of
`f(x)=x+4` is at x=-4 and end value is at x=3.

Starting value:
`f(-4)=-4+4=0`

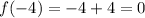
End value:
`f(3)=3+4=7`

Starting value of
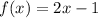`f(x)=2x-1` is at x=3 and end value is at x=6.

Starting value:
`f(3)=2(3)-1=5`

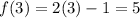
End value:
`f(6)=2(6)-1=11`

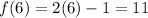
Least range value is 0 at x=-4 and 0 is included in the range because -4 is included in the domain.

Largest range value is 11 at x=6 and 11 is not included in the range because 6 is not included in the domain.

So, the range of the given piecewise function is [0,11).

Therefore, the correct option is A.