Question

Find the distance between the two points in simplest radical form.
(-5,8) and (-3, 1)

Answer 1

Given:

The two points are (-5,8) and (-3,1).

To find:

The distance between the given two points in simplest radical form.

Solution:

Distance formula: The distance between two points is

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

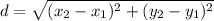
Using distance formula, the distance between (-5,8) and (-3,1) is

`d=√((-3-(-5))^2+(1-8)^2)`

`d=√((-3+5)^2+(-7)^2)`

`d=√((2)^2+(-7)^2)`

`d=√(4+49)`

`d=√(53)`

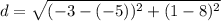
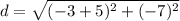
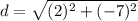
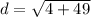
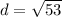
Therefore, the distance between two points (-5,8) and (-3,1) is
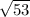`√(53)` units.