Question

Algebra 2

S varies inversely as G. If S is 8 when G is 3.5, find S when G is 7.
a) Write the variation.
b) Find S when G is 7.

Answer 1

a) S varies inversely as G

`S\propto(1)/(G)`

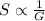
or
`S=(K)/(G)`

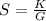
b) S=4 when G=7

Explanation:

a) Write the variation.

S varies inversely as G

`S\propto(1)/(G)`

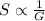
So, We can write:
`S=(K)/(G)`

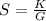
Where k is constant of proportionality

b) Find S when G is 7.

Now, if S=8, G = 3.5 we will find K

`S=(K)/(G)\\K=SG\\K=8* 3.5\\K=28`

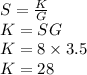
So, value of K= 28

Now, find S when G is 7

`S=(K)/(G)\\S=(28)/(7)\\S=4`

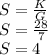
So, S=4 when G=7