Answer:
The function that models the total number of visitors at both parks each hour after sunrise:
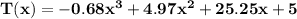
Option B is correct.
Explanation:
Function for West Park: A(X) =
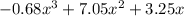
Function for East Park: B(x) =
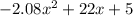
We need to find the function that models the total number of visitors at both parks each hour after sunrise?
For finding total number of visitors we need to sum functions of A(X) and B(X) to get T(X)
So, we have

So, function that models the total number of visitors at both parks each hour after sunrise:
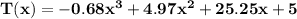
Option B is correct.