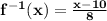Question

1.

For the function f(x) =
8x + 10, find the inverse function.
O
x2 - 10
f-4x) =
-,X20
8
O
(x - 10)2
f-1(x) =
x2 10
8
f-1(x)
X2 + 10
8
,*20
x2 - 10
f-4(x) =
-, X30
8

Answer 1

The answer is
`f^(-1)(x)= (x^(2) - 10)/(8), x > =0`

Answer 2

The inverse of
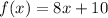`f(x)=8x+10` is
`\mathbf{f^(-1)(x)=(x-10)/(8)}`

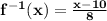
Explanation:

`f(x)=8x+10`

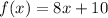
We need to find inverse of the function.

For finding inverse of function,

let
`y=8x+10`

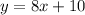
Now, solving to find value of x

Subtracting 10 on both sides

`y-10=8x+10-10\\y-10=8x`

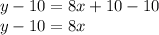
Divide both sides by 8

`(8x)/(8)=(y-10)/(8) \\x=(y-10)/(8)`

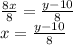
Now replace y with x and x with
`f^(-1)(x)`

`f^(-1)(x)=(x-10)/(8)`

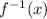
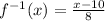
So, the inverse of
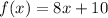`f(x)=8x+10` is
`\mathbf{f^(-1)(x)=(x-10)/(8)}`