Question

Which graph represents the solutions to the inequality |2x - 6 < 4? (5 points)

-9-8-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9
-9-8-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
9
-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9
-9-8-7 -6 -5 -4 -3 -2 -1
0 1 2 3 4 5 6 7 8 9

Answer 1

`\left|2x-6\right|<4\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:1<x<5\:\\ \:\mathrm{Interval\:Notation:}&\:\left(1,\:5\right)\end{bmatrix}`

Therefore, the 3rd graph represents the solutions to inequality.

Please also check the graph below.

Explanation:

Given the expression

`|2x\:-\:6|\:<\:4`

`\mathrm{Apply\:absolute\:rule}:\quad \mathrm{If}\:|u|\:<\:a,\:a>0\:\mathrm{then}\:-a\:<\:u\:<\:a`

`-4<2x-6<4`

`2x-6>-4\quad \mathrm{and}\quad \:2x-6<4`

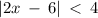
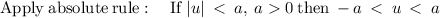
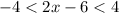
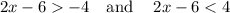
condition 1

`2x-6>-4`

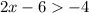
Add 6 to both sides

`2x-6+6>-4+6`

`2x>2`

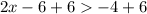
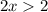
Divide both sides by 2

`(2x)/(2)>(2)/(2)`

`x>1`

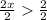
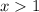
condition 2

`2x-6<4`

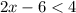
Add 6 to both sides

`2x-6+6<4+6`

`2x<10`

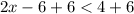
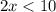
Divide both sides by 2

`(2x)/(2)<(10)/(2)`

`x<5`

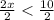
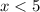
combine the intervals

`x>1\quad \mathrm{and}\quad \:x<5`

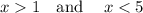
Merging overlapping intervals

`1<x<5`

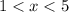
Thus,

`\left|2x-6\right|<4\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:1<x<5\:\\ \:\mathrm{Interval\:Notation:}&\:\left(1,\:5\right)\end{bmatrix}`

Therefore, the 3rd graph represents the solutions to inequality.

Please also check the graph below.