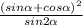Question

How to solve this ? I am not sure pls if you know the answer answer it I really neeed it for marks

Answer 1

L.S = R.S ⇒ Proved down

Explanation:

Let us revise some rules in trigonometry

1. sin²α + cos²α = 1
2. sin2α = 2 sin α cosα
3. cscα = 1/sinα

To solve the question let us find the simplest form of the right side and the left side, then show that they are equal

∵ L.S = csc2α + 1

→ By using the 3rd rule above

∴ L.S =
`(1)/(sin2\alpha)` + 1

→ Change 1 to
`(sin2\alpha)/(sin2\alpha)`

∴ L.S =
`(1)/(sin2\alpha)` +
`(sin2\alpha)/(sin2\alpha)`

→ The denominators are equal, then add the numerators

∴ L.S =
`(1+sin2\alpha)/(sin2\alpha)`

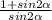
∵ R. S =
`((sin\alpha+cos\alpha)^(2) )/(sin2\alpha)`

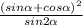
∵ (sinα + cosα)² = sin²α + 2 sinα cosα + cos²α

∴ (sinα + cosα)² = sin²α + cos²α + 2 sinα cosα

→ By using the 1st rule above, equate sin²α + cos²α by 1

∴ (sinα + cosα)² = 1 + 2 sinα cosα

→ By using the 2nd rule above, equate 2 sinα cosα by sin2α

∴ (sinα + cosα)² = 1 + sin2α

→ Substitute it in the R.S above

∴ R. S =
`(1+sin2\alpha)/(sin2\alpha)`

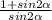
∵ L.S = R.S

∴ csc 2α + 1 =
`((sin\alpha+cos\alpha)^(2) )/(sin2\alpha)`