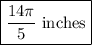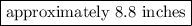To solve this problem, you will need to know the formula to find the circumference of a circle given the diameter of a circle. After calculating the circumference, you will then divide this result by 5 to obtain the final answer needed for this problem.
Find the Circumference
The circumference of a circle is found using the formula C = 2πr.
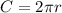
We are given the diameter. The radius can be found using r = D/2.
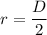
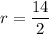

Plug in the radius to the formula for a circle's circumference: C = 2πr.
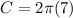
Rearrange the equation to distribute the 7 into the 2π.
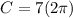
Distribute the 7.
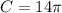
Find One-Fifth of the Distance
To find one-fifth of the distance (formally termed the circumference) around the circle, divide the circumference by 5.
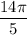
If you are looking for a simplified answer in terms of π, this will suffice. If you need an exact answer that does not reference π, continue reading.
For a solution not in terms of π, first, multiply 14 by π.
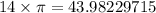
Divide this value by 5.
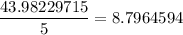
To make this easier to present, round to the hundredths place.
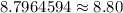
The final answer, dependent on the value you are asked to provide, is: