Answer: The function is odd and symmetric with respect to the origin.
Explanation:
A function is even if f(x)=f(-x), and odd if f(x)=-f(-x). If a function satisfies neither of these, it is neither even nor odd.
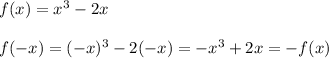
Therefore, the function is odd, and thus the function is symmetric about the origin