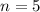Question

The graph shows the location of point P and point R. Point R is on the y-axis and has the same y-coordinate as point P. Point Q is graphed at (n,-2). The distance from point P to point Q is equal to the distance from point P to point R. What is the from point P to point Q? What is the value of N? Explain how you determined the distance from point P to point Q, and the value of N.

Answer 1

n = 5

Explanation:

Coordinate of P = (n,3)

R is on y-axis & the y-coordinate of P & R are equal. So coordinate of R = (3,0)

Coordinate of Q = (n,-2)

Using distance formula,

Distance between P & Q =

`\sqrt{ {( n - n}) ^(2) + {( 3- ( - 2) })^(2) }`

`= > \sqrt{ {(3 + 2)}^(2) } = \sqrt{ {5}^(2) } = 5`

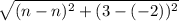
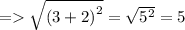
Distance between P & R =

`\sqrt{ {(n - 0)}^(2) + {(3 - 3)}^(2) }`

`= > \sqrt{ {n}^(2) } = n`

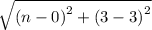
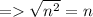
But in question it is given that distance between P & Q is equal to the distance between P & R. So,

`n = 5`