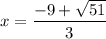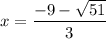Question

Solve the equation uding the most direct method: 3x(x+6)=-10?​

Answer 1

To solve this problem, you will use the distributive property to create an equation that can be rearranged and solved using the quadratic formula.

Distribute

Use the distributive property to distribute 3x into the term (x + 6):

`3x(x+6)=-10`

`3x^2+18x=-10`

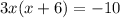
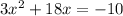
Rearrange

To create a quadratic equation, add 10 to both sides of the equation:

`3x^2+18x+10=-10+10`

`3x^2+18x+10=0`

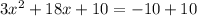
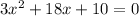
Use the Quadratic Formula

The quadratic formula is defined as:

`\displaystyle x = (-b \pm √(b^2 - 4ac))/(2a)`

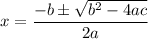
The model of a quadratic equation is defined as ax² + bx + c = 0. This can be related to our equation.

Therefore:

• a = 3
• b = 18
• c = 10

Set up the quadratic formula:

`\displaystyle x=(-18 \pm √((18)^2 - 4(3)(10)))/(2(3))`

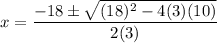
Simplify by using BPEMDAS, which is an acronym for the order of operations:

Brackets

Parentheses

Exponents

Multiplication

Division

Addition

Subtraction

Use BPEMDAS:

`\displaystyle x=(-18 \pm √(324 - 120))/(6)`

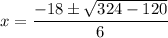
Simplify the radicand:

`\displaystyle x=(-18 \pm √(204))/(6)`

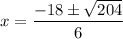
Create a factor tree for 204:

204 - 1, 2, 3, 4, 6, 12, 17, 34, 51, 68, 102 and 204.

The largest factor group that creates a perfect square is 4 × 51. Therefore, turn 204 into 4 × 51:

`√(4*51)`

Then, using the Product Property of Square Roots, break this into two radicands:

`√(4) * √(51)`

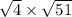
Since 4 is a perfect square, it can be evaluated:

`2 * √(51)`

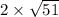
To simplify further for easier reading, remove the multiplication symbol:

`2√(51)`

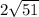
Then, substitute for the quadratic formula:

`\displaystyle x=(-18 \pm 2√(51))/(6)`

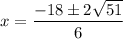
This gives us a combined root, which we should separate to make things easier on ourselves.

Separate the Roots

Separate the roots at the plus-minus symbol:

`\displaystyle x=(-18 + 2√(51))/(6)`

`\displaystyle x=(-18 - 2√(51))/(6)`

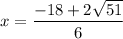
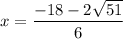
Then, simplify the numerator of the roots by factoring 2 out:

`\displaystyle x=(2(-9 + √(51)))/(6)`

`\displaystyle x=(2(-9 - √(51)))/(6)`

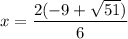
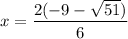
Then, simplify the fraction by reducing 2/6 to 1/3:

`\boxed{\displaystyle x=(-9 + √(51))/(3)}`

`\boxed{\displaystyle x=(-9 - √(51))/(3)}`

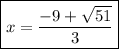
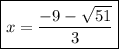
The final answer to this problem is:

`\displaystyle x=(-9 + √(51))/(3)`

`\displaystyle x=(-9 - √(51))/(3)`