Answer: (2, 3, 1)
This means x = 2, y = 3 and z = 1
========================================================
Work Shown:
Double everything in the second equation to get 4x-2y+4z=6
Add this result to the first equation
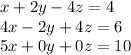
The first two lines of that expression above shows us adding x+2y-4z=4 to the equation 4x-2y+4z = 6
The x terms add to x+4x = 5x
The y terms add to 2y+(-2y) = 0y
The z terms add to -4z+4z = 0z
The terms on the right hand side add to 4+6 = 10
That's how we end up with the new equation 5x+0y+0z = 10
That becomes 5x = 10 which solves to x = 2 when we divide both sides by 5.
------------------------
Use this x value in the third original equation to find z
3x-8z = -2
3(2)-8z = -2
6-8z = -2
-8z = -2-6
-8z = -8
z = -8/(-8)
z = 1
------------------------
Use the x and z values we found to find y
x+2y-4z = 4
2+2y-4(1) = 4
2+2y-4 = 4
2y-2 = 4
2y = 4+2
2y = 6
y = 6/2
y = 3
----------------------
Overall we get the solutions to be x = 2, y = 3 and z = 1
We can say the solution as an ordered triple is (x,y,z) = (2,3,1)