Question

F(x)=x^2.what is g(x) ?

Answer 1

Option C.
`g(x)=((1)/(3)x)^2`

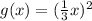
Explanation:

Stretch transformations of functions

In which direction is the transformation happening?

Given a function to start with, extra operations that are done outside of the given function, cause vertical transformations, whereas operations that are done inside of the function cause horizontal transformations.

Transformations on the outside

Ex.
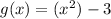`g(x)=(x^2)-3` is subtracting 3 outside, so its transformation is vertical.

Transformations on the inside

Ex.
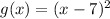`g(x)=(x-7)^2` is subtracting 7 inside, so its transformation is horizontal.

Stretch/compression transformations

For any function, stretches or compressions occur by multiplying by positive numbers larger or smaller than 1.

Multiplying by numbers larger than one, quantities get larger, and multiplying by a positive number less than one, quantities get smaller.

For example,
`\$10*2 = \$20`, but
`\$10*(1)/(2) = \$5`

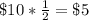
For transformations, this intuition needs a small modification:

• Operations outside: transformations happen "normally" as you would expect.
• Operations inside: transformations happen "backwards" from the natural way one might expect.

Multiplying on the outside

When multiplying outside of the function, things outside happen normally, and since it is happening outside, it is in a vertical direction.

Ex. Multiplying outside by 3, things get larger (stretch) vertically to 3 times as much as (300% of) normal (away from a height of zero).

Multiplying outside by
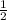`(1)/(2)` , things get smaller (compress) vertically down to
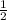`(1)/(2)` as much as (50% of) normal (toward a height of zero).

"g" is lower than "f", so it may have been compressed vertically (see alternative solution at end).

Looking at the only options with multiplication outside (A & B), option B multiplies by 3 (greater than 1), so it would stretch "f" even taller.

Option A, does compress "f" vertically (by 1/3), but doesn't compress it enough to arrive at the point (3,1) defined on function "g". Note ordered pair (3,1) on "g", meaning when you input "3", you get out "1".

Putting 3 into the "f" function, f(3)=9. Since one-third (the transformation in Option A) of 9 is 3, not 1, Option A doesn't compress "f" enough.

Multiplying on the inside

When multiplying inside, transformations happen horizontally, and inside things happen "backwards".

So, if multiplying inside by 4, (...normally things get bigger...) things actually get smaller (compressed) horizontally, reduced to 1/4 (the reciprocal of 4) the size (toward a horizontal distance of zero).

If multiplying by a number less than one (but positive), like
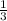`(1)/(3)` , (...things normally get smaller...) things will actually get larger (stretch) in the horizontal direction out to triple (the reciprocal of
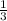`(1)/(3)`) as much as normal.

Looking options C & D (where multiplication happens inside), both have multiplication by a positive number less than one (... normally would make things smaller...), which will stretch "f" out horizontally.

How far has the function been stretched out horizontally?

Looking at the red point (3,1), the blue function does have a height-matched point at (1,1).

Measuring horizontal distances, (3,1) is 3-units from the y-axis, whereas (1,1) is only 1-unit away. Thus, the "g" is 3 times as far as "f", meaning a horizontal stretch outward by 3.

Answer C multiplies inside by
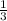`(1)/(3)`, so it actually makes things 3 times bigger horizontally.

The correct answer is option C.

Verifying algebraically

To verify, from (3,1), put 3 into the option C g(x) -- it gives "1" as an output.

`g(x)=((1)/(3)x)^2\\g(3)=((1)/(3)(3))^2\\g(3)=(1)^2\\g(3)=1\\`

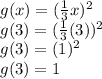
An alternative solution

This function could have been compressed vertically to obtain the red graph.

Note that f(3)=9.

The point (3,1), on the red function, is only at a height of 1 ... 1/9th the height of the blue function. We could compress the "f" vertically by 1/9th to transform the blue function into the red function.

Vertical transformations come from operations outside, and outside things behave "normally", so to vertically compress by 1/9th, just multiply on the outside by 1/9th.

Thus, an alternative answer to transform f(x) to g(x) is
`g(x)=(1)/(9)(x^2)`

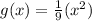
Two last things:

Simplifying this function we just obtained we get
`g(x)=(1)/(9)x^2`

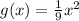
Returning to the function that we chose for our answer in option C,
`g(x)=((1)/(3)x)^2`

`g(x)=((1)/(3)x)((1)/(3)x)`

`g(x)=(1)/(9)x^2`

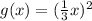
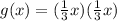
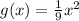
Note that the transformation answer for this problem (Option C) and our alternative solution both simplify and match perfectly, so they both represent the same end result.