-------------------------------------------------------------------------------------------------------------
Answer:

-------------------------------------------------------------------------------------------------------------
Given:
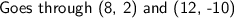
Find:

Solution: In order to determine the slope of the line we need to use the slope formula where we just plug in the values and simplify.
Plug in the values
Simplify the expression
Therefore, the slope of the line that fits the description that was provided in the problem statement is -3.