Answer:
a)
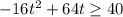
b)
![[2-(√(6))/(2) , 2+(√(6))/(2)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/9r745edv45wmqiqy8ud5vt1179wqxhzml0.png)
(see attached picture for the number line)
This interval means that from about 0.78s to about 3.22s the ball will not be visible because it will be higher than 40 feet high.
c)
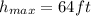
d) t=2s
Explanation:
a)
Basically the ball will disappear when it is higher than 40 ft, so we can build the inequality like this:
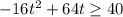
this is because the function represents it's height, so when the function is greater than or equal to 40, then the ball will disappear.
b) to solve the inequality, first we need to turn the ≥ symbol to an = symbol and solve for t, so we get:
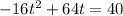
we can move the 40 to the other side of the equation so we get:
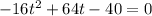
we can factor the equation so it's easier to solve, so we get:
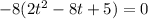
which simplifies to:
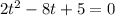
and we can use the quadratic formula to solve this equation, so we get:
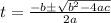
so we get:
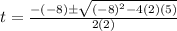
which yields:

and next we need to test the posible intervals to see which one makes the inequality true, the possible intervals are:
![(-\infty, 2-(√(6))/(2)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/fqbd4sew9t0nnenx2jqa5v7qx27apr4mp2.png) for a test value of 0
for a test value of 0
![[2-(√(6))/(2),2+(√(6))/(2)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/8c45wqnuwf8ttxqq88ra919ke19o0bbpr2.png) for a test value of 1
for a test value of 1
 for a test value of 4
for a test value of 4
so next we test each of the values in the original inequality and see if the inequality is true:
![(-\infty, 2-(√(6))/(2)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/fqbd4sew9t0nnenx2jqa5v7qx27apr4mp2.png) for a test value of 0
for a test value of 0

 false
false
so this is not an answer.
![[2-(√(6))/(2),2+(√(6))/(2)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/8c45wqnuwf8ttxqq88ra919ke19o0bbpr2.png) for a test value of 1
for a test value of 1
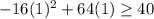
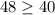
true, so this is an answer.
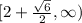 for a test value of 4
for a test value of 4
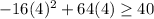
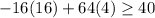
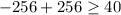

false, so this is no answer.
So the answer is the interval:
![[2-(√(6))/(2),2+(√(6))/(2)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/8c45wqnuwf8ttxqq88ra919ke19o0bbpr2.png)
This interval means that from about 0.78s to about 3.22s the ball will not be visible because it will be higher than 40 feet high.
c) In order to find how high Penelope kick the football, we must find the vertex of the parabola which is gotten when graping the given function (see attached picture)
so we can use the following formula to find the t-value for this maximum height:
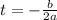
so we substitute the corresponding values:

which yields:
t=2s
next, we can substitute this time into the original function to find the maximum height, so we get:

which yields:
h=64 ft
d) We found the answer for d on the previous part where we got that t=2s