Question

Which best describes the effect on the x-intercept of the graph of y=34x−3 if the slope is changed to −34

The x-intercept remains the same and the new line is translated upwards


The x-intercept becomes negative and the new line is parallel to the original line


The x-intercept remains the same and the new line is translated downward


The x-intercept becomes negative and the new line intersects the original line

Answer 1

Explanation:

⊕ The x-intercept becomes negative and the new line intersects the original line { at (0, - 3) }

Answer 2

The last option: The x-intercept becomes negative and the new line intersects the original line.

Explanation:

Remember that when finding the x-intercept you set y to 0.

Let's compare the two equations when we solve for x:

0=34x-3 0=-34x-3

1. Add 3 to both sides of the equations

3=34x 3=-34x

2. Divide the coefficients

`(3)/(34)`=x
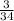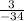`(3)/(-34)`=x

We know that the new slope does not remain the same as stated in the first and third options. In order for two lines to be parallel, the slopes must be exactly the same, so the second option is incorrect. Therefore, the last option is correct.